12. High Performance Computing (part I: OpenMP)#
Parallel computing overview
OpenMP threading model
OpenMP directives
Basic techniques in OpenMP:
loop parallelization, parallel sections synchronization constructsLab exercises with OpenMP
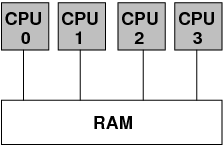
12.1. Parallel vs Serial computing#
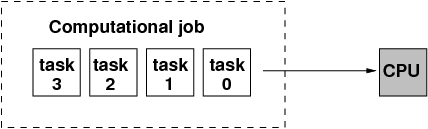
Computational tasks are processed in sequential order, essentially, on one CPU core.
Doesn’t take advantage of the modern multi-core architectures.
Computational tasks are processed concurrently on the different CPUs or cores
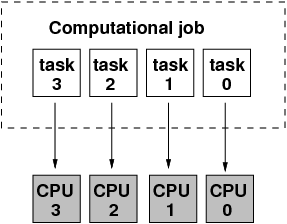
The tasks can be different executable codes, code blocks, loops, subroutines, I/O calls, etc.
The platform can be a single multi-core host or a computational cluster of network interconnected hosts or combination of both.
Special programming methods and software are required, for example, OpenMP or MPI.
12.3. Parallel computing paradigms: distributed memory#
Distributed memory: the CPUs have access only to their own memory space. Data is exchanged via messages passed over the network.
The network can be various: Ethernet, Infiniband, OmniPath
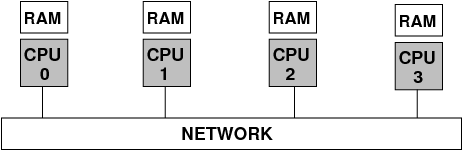
Programming approach: Message Passing Interface (MPI)
12.4. Parallel computing paradigms: Hardware acceleration#
Hardware acceleration: some tasks are offloaded from CPU onto a multi-core GPU device. Data is transferred over a PCIe bus between the RAM and GPU.
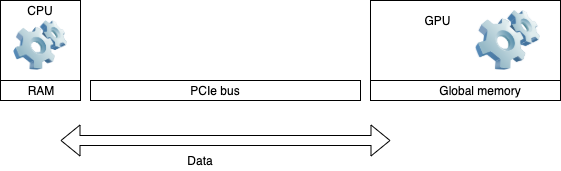
Programming approach: CUDA, OpenCL, OpenACC. The latest OpenMP, 5.0, supports offloading to accelerator devices.
12.5. Parallel code speedup#
In practice, usually only a part of a code can be efficiently parallelized.
Amdahl’s law imposes a theoretical limit on a parallel code speedup:
Speedup = \({Wall \; clock \; time \; of \; serial \; execution}\over{Wall \; clock \; time \; of \; parallel \; execution}\) = \(1 \over{S + {{P}\over{N}}}\)
Where \(S\) is the scalar portion of the work,
\(P\) is the parallel portion of the work,
and \(N\) is the number of CPUs or cores.
By normalization, \(S + P = 1\)
For example, if only 50% of a code can be parallelized, its theoretical speedup can’t exceed the factor of two, according to the Amdahl’s law.
import numpy as np
import matplotlib.pyplot as plt
def graph(formula, x_range):
x = np.array(x_range)
y = eval(formula)
plt.xlabel('Number of CPU cores')
plt.ylabel('Speedup')
plt.title('Amdahl\'s law')
plt.xlim(1,100)
plt.plot(x, y)
plt.show()
graph('1/(0.5 + 0.5/x)', range(1, 100))
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[1], line 2
1 import numpy as np
----> 2 import matplotlib.pyplot as plt
3 def graph(formula, x_range):
4 x = np.array(x_range)
ModuleNotFoundError: No module named 'matplotlib'
As you can see on the graph above, it doesn’t make much sense utilizing more than 12 CPU cores for running the code since we may be able to reach about 90% of the maximum theoretical speedup on just 12 cores.
12.7. What is OpenMP#
OpenMP is an API environment for shared memory computer architectures.
It is implemented in the compilers, C/C++, and Fortran, through compiler directives, runtime libraries routines, and environment variables.
Thread based parallelism: multiple threads concurrently compute tasks in the same code.
Fork-join thread dynamics: the master thread forks a team of threads in a parallel region, then the threads terminate upon exiting the parallel region.
Defined data scoping: shared or private to the threads.
12.8. OpenMP workflow schematic#
Shared memory is used by parallel threads.
The master process forks threads in the parallel region of the code.
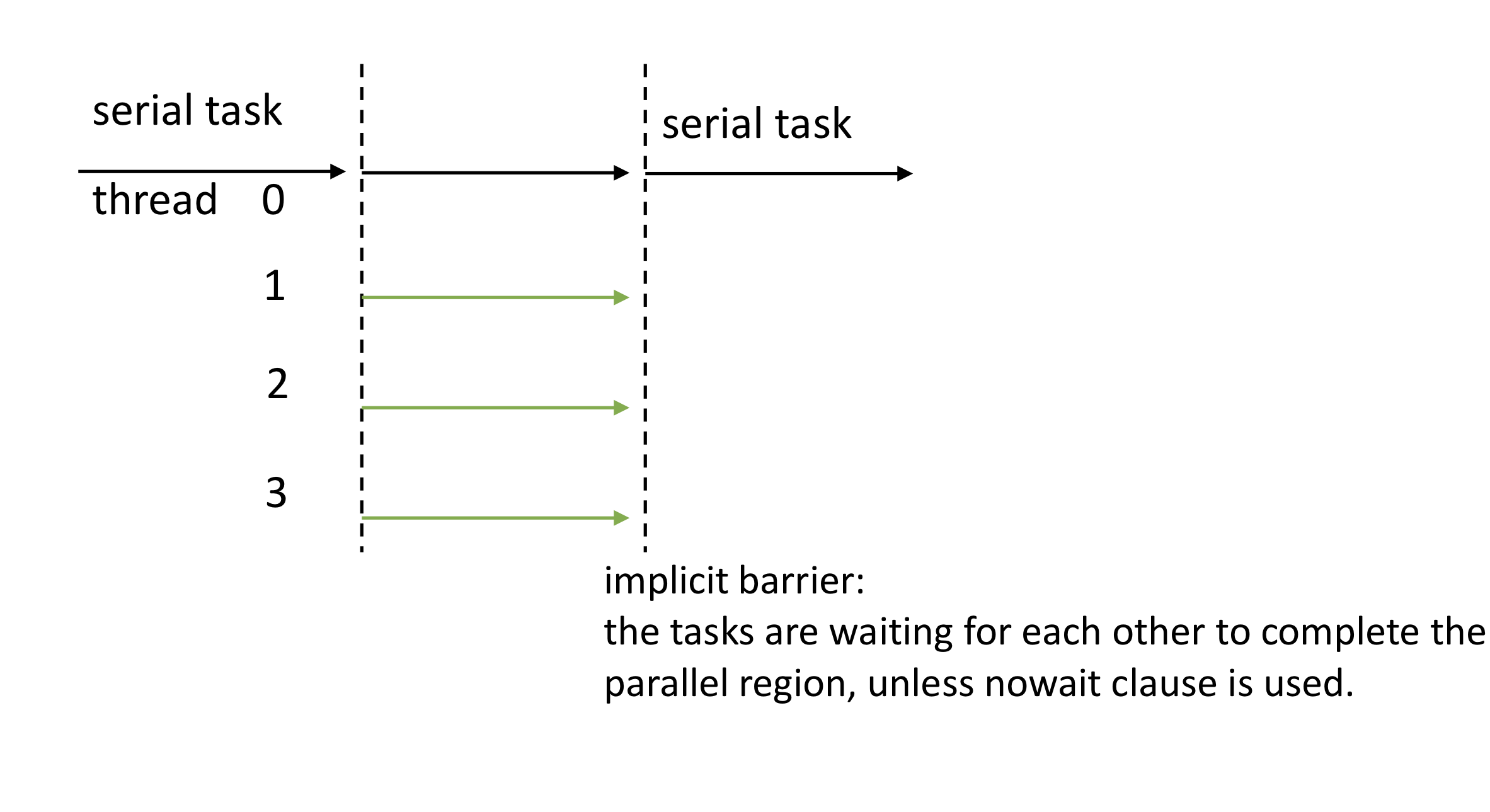
12.9. C/C++ general code structure with OpenMP compiler directives:#
int main() {
int var1, var2;
float var3;
/* Serial code */
/* Beginning of parallel section. Fork a team of threads. Specify variable scoping */
#pragma omp parallel private(var1, var2) shared(var3)
{
/* Parallel section executed by all threads */
/* All threads join master thread and disband */
}
/* Resume serial code */
}
12.10. OpenMP code compilation#
Recent gcc and gfortran compilers include OpenMP support.
gcc -fopenmp testcode.c
export OMP_NUM_THREADS=4
./a.out
Usually, OMP_NUM_THREADS shouldn’t exceed the total number of available cores in a system.
If OMP_NUM_THREADS is undefined, the run will utilize all available cores on the system.
12.11. OpenMP compiler directives – pragma, constructs, clauses#
#pragma omp construct [clause [clause]…]
For example:
#pragma omp parallel shared(a,b,c) private(i)
#pragma omp sections nowait
#pragma omp section
#pragma omp for
The constructs specify what the threads should do, for example:
Compute concurrently blocks/sections of a code,#pragma omp section
Compute concurrently distributed chunks of loop iterations,#pragma omp for
Thread synchronization,#pragma omp critical
The clauses define the parameters for the constructs, for example:
Variable scope (private for each thread),private(i)
Variable scope (shared for the threads),shared(a,b,c)
Scheduling directives,nowait, schedule
Synchronization related directives,critical, reduction
12.12. The runtime library functions#
They set and query parameters for the threads, for example
omp_get_num_threads – returns the number of threads in the running team.
omp_get_thread_num – returns the thread number
There are 57 run time library functions in the OpenMP in gcc 7.5:
egrep 'omp_.*\(' $(find /usr -name omp.h)
12.13. Parallel regions (exercise)#
Simple “Hello World” program. Every thread executes all code enclosed in the parallel section. OpenMP library routines are used to obtain thread identifiers and total number of threads.
#include <omp.h>
#include <stdio.h>
int main () {
int nthreads, tid;
/* Fork a team of threads with each thread having a private tid variable */
#pragma omp parallel private(tid)
{
/* Obtain and print thread id */
tid = omp_get_thread_num();
printf("Hello World from thread = %d\n", tid);
/* Only master thread does this */
if (tid == 0)
{
nthreads = omp_get_num_threads();
printf("Number of threads = %d\n", nthreads);
} /* All threads join master thread and terminate */
}
}
Copy the content of the code above into file hello.c, then compile and run it across 4 threads as follows:
gcc -fopenmp -o hello.x hello.c
export OMP_NUM_THREADS=4
./hello.x
12.14. Parallel loops#
A simple work sharing construct: parallel loops
export OMP_NUM_THREADS=4
/* Fork a team of threads with private i , tid variables */
#pragma omp parallel private(i, tid)
{
same_work();
// Compute the for loop iteractions in parallel
#pragma omp for
for (i=0; i<=4*N-1; i++)
{
thread(i); //should be a thread safe function
} //the final results are independent on the order of the
} //loop iteration

12.15. The for loop construct#
Since the parallel region has been defined, the iterations of the loop must be executed in parallel by the team.
#pragma omp for [clause ...]
schedule (type [,chunk]) //how the loop iterations assigned to threads
private (list) //the variable scope private to the threads
shared (list). //the variable scope shared to the threads
reduction (operator: list) //if reduction is applied to the total value
collapse (n) //in case of nested loop parallelization
nowait //if set, the threads do not synchronize at the end of the parallel loop
There are other possible clauses in the for construct not discussed here.
12.16. The for loop schedule clause#
Describes how the iterations of the loop are divided among the threads in the team.
STATIC: loop iterations are divided into pieces of size chunk and then statically assigned to the threads.
DYNAMIC: the chunks, and dynamically scheduled among the threads; when a thread finishes one chunk, it is dynamically assigned another. The default chunk size is 1.
GUIDED: similar to DYNAMIC except that the block size decreases each time a parcel of work is given to a thread.
RUNTIME: defined by the environment variable OMP_SCHEDULE
AUTO: the scheduling decision is delegated to the compiler and/or runtime system.
12.17. The for loop (exercise)#
The loop iterations computed concurrently.
#include <stdio.h>
#include <omp.h>
#define CHUNKSIZE 100
#define N 1000
int main ()
{
int i, chunk, tid;
float a[N], b[N], c[N];
/* Some initializations */
for (i=0; i < N; i++)
a[i] = b[i] = i * 1.0;
chunk = CHUNKSIZE;
#pragma omp parallel shared(a,b,c,chunk) private(i)
#pragma omp for schedule(dynamic,chunk) nowait
for (i=0; i < N; i++)
{
c[i] = a[i] + b[i];
/* Obtain and print thread id and array index number */
tid = omp_get_thread_num();
printf("thread = %d, i = %d\n", tid, i);
} /* end of parallel section */
}
Copy the content of the code above into file for.c, then compile and run it as follows:
gcc -fopenmp -o for.x for.c
export OMP_NUM_THREADS=4
./for.x
Run ./for.x several times and observe how the array elements are distributed across the threads.
12.18. Nested loops#
By default only the outer loop is parallelized:
#pragma omp parallel for
for (int i=0;i<N;i++)
{
for (int j=0;j<M;j++)
{
/* do task(i,j) */
}
}
To parallelize both the loops:
#pragma omp parallel for collapse(2)
for (int i=0;i<N;i++)
{
for (int j=0;j<M;j++)
{
/* do task(i,j) */
}
}
12.19. Parallel sections (exercise)#
Independent SECTION directives are nested within a SECTIONS directive. Each SECTION is executed once by a thread in the team. Different sections may be executed by different threads. It is possible that for a thread to execute more than one section if it is quick enough and the implementation permits such.
#include <omp.h>
#include <stdio.h>
#define N 1000
int main ()
{ int i, tid;
float a[N], b[N], c[N], d[N];
/* Some initializations */
for (i=0; i < N; i++) {
a[i] = i * 1.5;
b[i] = i + 22.35;
}
#pragma omp parallel shared(a,b,c,d) private(i)
{
#pragma omp sections nowait
{
#pragma omp section
{
for (i=0; i < N; i++)
c[i] = a[i] + b[i];
/* Obtain and print thread id and array index number */
tid = omp_get_thread_num();
printf("thread = %d, i = %d\n", tid, i);
}
#pragma omp section
{
for (i=0; i < N; i++)
d[i] = a[i] * b[i];
/* Obtain and print thread id and array index number */
tid = omp_get_thread_num();
printf("thread = %d, i = %d\n", tid, i);
}
} /* end of sections */
} /* end of parallel section */
}
Copy the content of the code above into file sections.c, then compile and run it as follows:
gcc -fopenmp -o sections.x sections.c
export OMP_NUM_THREADS=2
./sections.x
Run ./sections.x several times and observe how the code sections are distributed across the threads.
12.20. When things become messy#
Several threads are updating the same variable.
#pragma omp parallel for shared (sum) private (i)
for ( int i=0; i < 1000000; i++) {
sum = sum + a[i];
}
printf("sum=%lf\n",sum);
The threads overwrite the sum variable for each other, running into the “race condition”.
The problem can be solved by using critical locks and critical sections, when only one thread at a time updates the sum.
12.21. Synchronization construct#
#pragma omp parallel for shared (sum) private (i)
for ( int i=0; i < 1000000; i++) {
#pragma omp critical
sum = sum + a[i];
}
printf("sum=%lf\n",sum);
The critical section specifies a region of a code that must be executed by only one thread at a time.
12.22. Syncronization construct (exercise)#
Create a new directory for exercises. Download a tar ball into the directory. Extract the files:
mkdir OpenMP
cd OpenMP
wget https://linuxcourse.rutgers.edu/2024/html/lessons/HPC_1/OpenMP.tgz
tar -zxvf OpenMP.tgz
Compile sum.c with the -fopenmp and run executable across 2 threads:
export OMP_NUM_THREADS=2
gcc -fopenmp -o sum.x sum.c
./sum.x
Modify file sum.c and remove the line with the construct critical. Recompile it again and run several times. Notice the different output results.
12.23. Reduction clause#
Scalar product of two vectors, \(\vec{A}\) and \(\vec{B}\):
result = \((\vec{A} \cdot \vec{B})\) = \(A_0 \cdot B_0 + A_1 \cdot B_1 + … + A_{n-1} \cdot B_{n-1} \)
Have each thread to compute partial sums, result, on a chunk of data.
#pragma omp parallel for \
default(shared) private(i) \
schedule(static,chunk) \
reduction(+:result)
for (i=0; i < n; i++)
result = result + (a[i] * b[i]);
A private copy for variable result is created for each thread. At the end of the reduction, the reduction variable is written in the global shared variable.
12.24. Reduction clause (exercise)#
In directory OpenMP compile reduction.c and execute in 4 threads:
gcc -fopenmp -o reduction.x reduction.c
export OMP_NUM_THREADS=4
./reduction.x
12.25. Constructs for single thread execution in parallel region#
Only by the master thread:
#pragma omp master
{
printf( "iteration %d, toobig=%d\n", c, toobig );
}
Only by any single thread:
#pragma omp single
{
printf ("Outer: num_thds=%d\n", omp_get_num_threads());
}
12.26. The atomic construct#
The omp atomic construct allows access of a specific memory location atomically, avoiding race conditions. Here it simultaneous updates of an element of x by multiple threads.
#pragma omp parallel for shared(x, y, index, n)
for (i=0; i<n; i++) {
#pragma omp atomic update
x[index[i]] += work1(i);
y[i] += work2(i);
}
Note that the atomic directive applies only to the statement immediately following it. As a result, elements of y are not updated atomically in this example.
12.27. Synchronization construct barrier#
#pragma omp barrier
The omp barrier directive identifies a synchronization point at which threads in a parallel region will wait until all other threads in that section reach the same point. Statement execution past the omp barrier point then continues in parallel.
12.28. Physical problem formulation#
Heated 2D Plate problem
The physical 2D region, and the boundary conditions, are suggested by this diagram.
Need to find a steady state temperature distribution, W(x,y)
W = 0
+------------------+
| |
W = 100 | | W = 100
| |
+------------------+
W = 100
12.29. Numerical discretization#
Numerical discretization: a grid with M x N nodes
I = 0
[0][0]-------------[0][N-1]
| |
J = 0 | | J = N-1
| |
[M-1][0]-----------[M-1][N-1]
I = M-1
Computational approach:
temperature at a grid point is averaged between that in the neighboring points
convergence to the steady state by Jacobi iterations:
while ( epsilon <= diff ) {
w[i][j] = ( u[i-1][j] + u[i+1][j] + u[i][j-1] + u[i][j+1] ) / 4.0;
diff = max|w[i][j] - u[i][j]|;
u[i][j] = w[i][j];
iterate++; }
12.30. OpenMP approach through loop parallelization#
The temperature, w, update via iteration:
# pragma omp for
for ( i = 1; i < M - 1; i++ )
{
for ( j = 1; j < N - 1; j++ )
{
w[i][j] = ( u[i-1][j] + u[i+1][j] + u[i][j-1] + u[i][j+1] ) / 4.0;
}
}
}
Iteration convergence factor estimate, diff:
# pragma omp parallel shared ( diff, u, w ) private ( i, j, my_diff )
{ my_diff = 0.0;
# pragma omp for
for ( i = 1; i < M - 1; i++ )
{ for ( j = 1; j < N - 1; j++ )
{
if ( my_diff < fabs ( w[i][j] - u[i][j] ) )
{
my_diff = fabs ( w[i][j] - u[i][j] );
}
}
}
# pragma omp critical
{ if ( diff < my_diff )
{
diff = my_diff;
}
}
}
When diff becomes smaller than a defined accuracy, the temperature in the box is considered converged to a steady state. The iterations are done.
12.31. CPU core number and performance (exercise)#
Find out the number of CPU cores available on your desktop:
grep processor /proc/cpuinfo
In the output, you should see ‘processor : 0’, … ‘processor : 7’, which means there are eight CPU threads available, and you can utilize them for running two OpenMP threads concurrently.
Alternatively, you can run command lscpu
lscpu
Download a source file with a C code for solving the steady state heat equation on a rectangular region:
wget http://linuxcourse.rutgers.edu/2024/html/lessons/HPC_1/heated_plate_openmp.c
Compile the source code with OpenMP:
gcc -fopenmp -o heated_plate.x heated_plate_openmp.c -lm
Run the compiled executable, heated_plate.x, with one thread:
export OMP_NUM_THREADS=1
./heated_plate.x > heated_plate_local_gcc_output.txt
While the application is running, open another console terminal and run command top. It shows the CPU and RAM utilization, as well as the most resource consuming processes. Type “1” to see the utilization of all the CPU cores. Type “H” to see all the process threads.
Run it with 2 threads:
export OMP_NUM_THREADS=2
./heated_plate.x >> heated_plate_local_gcc_output.txt
Run it with 4 threads:
export OMP_NUM_THREADS=4
./heated_plate.x >> heated_plate_local_gcc_output.txt
Repeat runs for cases OMP_NUM_THREADS=6, 8, 10.
The output results in the six runs above have been written in file heated_plate_local_gcc_output.txt
Compare the run time (Wallclock time) in the above cases:
grep Wallclock heated_plate_local_gcc_output.txt
Notice that the shortest Wallclock time was achieved in the 2 thread run , about 12.3 sec, almost three times faster than in the serial case, one core run. The CPUs on the virtual desktops have 4 physical cores. In case of the 8, 10 and 16 threads, the run took longer due to a slight overhead caused by the thread competition for the two CPU cores.